Z-Transform has following properties:
Linearity Property
If $,x (n) stackrel{mathrm{Z.T}}{longleftrightarrow} X(Z)$
and $,y(n) stackrel{mathrm{Z.T}}{longleftrightarrow} Y(Z)$
Then linearity property states that
$a, x (n) + b, y (n) stackrel{mathrm{Z.T}}{longleftrightarrow} a, X(Z) + b, Y(Z)$
Time Shifting Property
If $,x (n) stackrel{mathrm{Z.T}}{longleftrightarrow} X(Z)$
Then Time shifting property states that
$x (n-m) stackrel{mathrm{Z.T}}{longleftrightarrow} z^{-m} X(Z)$
Multiplication by Exponential Sequence Property
If $,x (n) stackrel{mathrm{Z.T}}{longleftrightarrow} X(Z)$
Then multiplication by an exponential sequence property states that
$a^n, . x(n) stackrel{mathrm{Z.T}}{longleftrightarrow} X(Z/a)$
Time Reversal Property
If $, x (n) stackrel{mathrm{Z.T}}{longleftrightarrow} X(Z)$
Then time reversal property states that
$x (-n) stackrel{mathrm{Z.T}}{longleftrightarrow} X(1/Z)$
Differentiation in Z-Domain OR Multiplication by n Property
If $, x (n) stackrel{mathrm{Z.T}}{longleftrightarrow} X(Z)$
Then multiplication by n or differentiation in z-domain property states that
$ n^k x (n) stackrel{mathrm{Z.T}}{longleftrightarrow} [-1]^k z^k{d^k X(Z) over dZ^K} $
Convolution Property
If $,x (n) stackrel{mathrm{Z.T}}{longleftrightarrow} X(Z)$
and $,y(n) stackrel{mathrm{Z.T}}{longleftrightarrow} Y(Z)$
Then convolution property states that
$x(n) * y(n) stackrel{mathrm{Z.T}}{longleftrightarrow} X(Z).Y(Z)$
Correlation Property
If $,x (n) stackrel{mathrm{Z.T}}{longleftrightarrow} X(Z)$
and $,y(n) stackrel{mathrm{Z.T}}{longleftrightarrow} Y(Z)$
Then correlation property states that
$x(n) otimes y(n) stackrel{mathrm{Z.T}}{longleftrightarrow} X(Z).Y(Z^{-1})$
Initial Value and Final Value Theorems
Initial value and final value theorems of z-transform are defined for causal signal.
Initial Value Theorem
For a causal signal x(n), the initial value theorem states that
$ x (0) = lim_{z to infty }X(z) $
This is used to find the initial value of the signal without taking inverse z-transform
Final Value Theorem
For a causal signal x(n), the final value theorem states that
$ x ( infty ) = lim_{z to 1} [z-1] X(z) $
This is used to find the final value of the signal without taking inverse z-transform.
Region of Convergence (ROC) of Z-Transform
The range of variation of z for which z-transform converges is called region of convergence of z-transform.
Properties of ROC of Z-Transforms
-
ROC of z-transform is indicated with circle in z-plane.
-
ROC does not contain any poles.
-
If x(n) is a finite duration causal sequence or right sided sequence, then the ROC is entire z-plane except at z = 0.
-
If x(n) is a finite duration anti-causal sequence or left sided sequence, then the ROC is entire z-plane except at z = ∞.
-
If x(n) is a infinite duration causal sequence, ROC is exterior of the circle with radius a. i.e. |z| > a.
-
If x(n) is a infinite duration anti-causal sequence, ROC is interior of the circle with radius a. i.e. |z| < a.
-
If x(n) is a finite duration two sided sequence, then the ROC is entire z-plane except at z = 0 & z = ∞.
The concept of ROC can be explained by the following example:
Example 1: Find z-transform and ROC of $a^n u[n] + a^{-}nu[-n-1]$
$Z.T[a^n u[n]] + Z.T[a^{-n}u[-n-1]] = {Z over Z-a} + {Z over Z {-1 over a}}$
$$ ROC: |z| gt a quadquad ROC: |z| lt {1 over a} $$
The plot of ROC has two conditions as a > 1 and a < 1, as you do not know a.
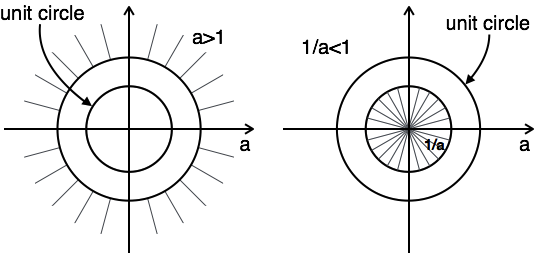
In this case, there is no combination ROC.
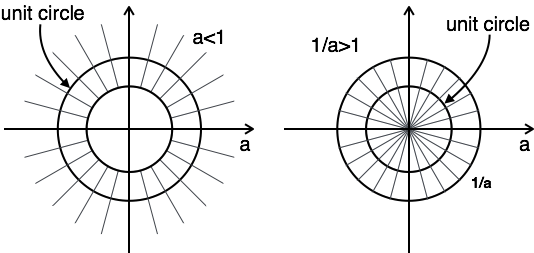
Here, the combination of ROC is from $a lt |z| lt {1 over a}$
Hence for this problem, z-transform is possible when a < 1.
Causality and Stability
Causality condition for discrete time LTI systems is as follows:
A discrete time LTI system is causal when
-
ROC is outside the outermost pole.
-
In The transfer function H[Z], the order of numerator cannot be grater than the order of denominator.
Stability Condition for Discrete Time LTI Systems
A discrete time LTI system is stable when
-
its system function H[Z] include unit circle |z|=1.
-
all poles of the transfer function lay inside the unit circle |z|=1.
Z-Transform of Basic Signals
| x(t) | X[Z] |
|---|---|
| $delta$ | 1 |
| $u(n)$ | ${Zover Z-1}$ |
| $u(-n-1)$ | $ -{Zover Z-1}$ |
| $delta(n-m)$ | $z^{-m}$ |
| $a^n u[n]$ | ${Z over Z-a}$ |
| $a^n u[-n-1]$ | $- {Z over Z-a}$ |
| $n,a^n u[n]$ | ${aZ over |Z-a|^2}$ |
| $n,a^n u[-n-1] $ | $- {aZ over |Z-a|^2}$ |
| $a^n cos omega n u[n] $ | ${Z^2-aZ cos omega over Z^2-2aZ cos omega +a^2}$ |
| $a^n sin omega n u[n] $ | $ {aZ sin omega over Z^2 -2aZ cos omega +a^2 } $ |
Learning working make money