Here are a few basic signals:

Unit Step Function

Unit step function is denoted by u(t). It is defined as u(t) = $left{begin{matrix}1 & t geqslant 0\ 0 & t

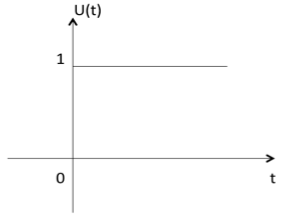
• It is used as best test signal.
• Area under unit step function is unity.

Unit Impulse Function

Impulse function is denoted by δ(t). and it is defined as δ(t) = $left{begin{matrix}1
& t = 0\ 0
& tneq 0
end{matrix}right.$

$$ int_{-infty}^{infty} δ(t)dt=u (t)$$

$$ delta(t) = {du(t) over dt } $$

Ramp Signal

Ramp signal is denoted by r(t), and it is defined as r(t) = $left{begin {matrix}t
& tgeqslant 0\ 0
& t

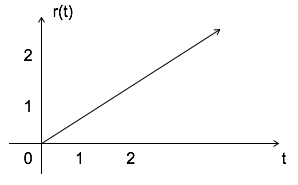
$$ int u(t) = int 1 = t = r(t) $$

$$ u(t) = {dr(t) over dt} $$

Area under unit ramp is unity.

Parabolic Signal

Parabolic signal can be defined as x(t) = $left{begin{matrix} t^2/2
& t geqslant 0\ 0
& t

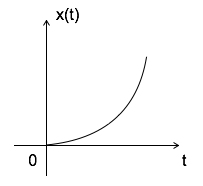
$$iint u(t)dt = int r(t)dt = int t dt = {t^2 over 2} = parabolic signal $$

$$ Rightarrow u(t) = {d^2x(t) over dt^2} $$

$$ Rightarrow r(t) = {dx(t) over dt} $$

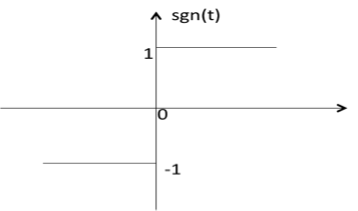
Signum Function

Signum function is denoted as sgn(t). It is defined as sgn(t) = $ left{begin{matrix}1
& t>0\ 0
& t=0\ -1
& t

Exponential Signal

Exponential signal is in the form of x(t) = $e^{alpha t}$.

The shape of exponential can be defined by $alpha$.

Case i: if $alpha$ = 0 $to$ x(t) = $e^0$ = 1

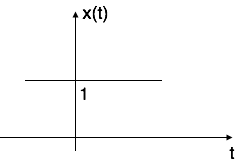
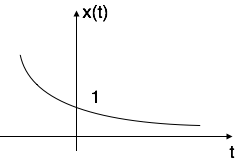
Case ii: if $alpha$

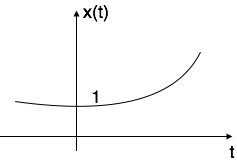
Case iii: if $alpha$ > 0 i.e. +ve then x(t) = $e^{alpha t}$. The shape is called raising exponential.

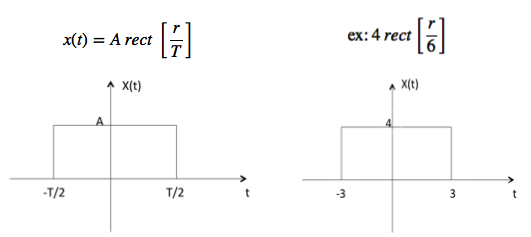
Rectangular Signal

Let it be denoted as x(t) and it is defined as

Triangular Signal

Let it be denoted as x(t)

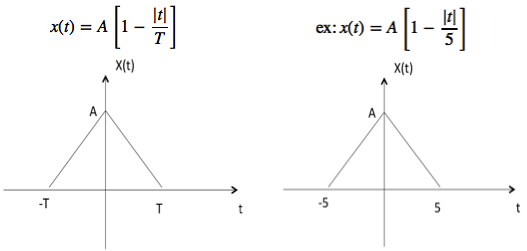
Sinusoidal Signal

Sinusoidal signal is in the form of x(t) = A cos(${w}_{0},pm phi$) or A sin(${w}_{0},pm phi$)

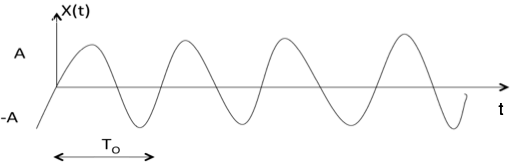
Where T₀ = $ 2pi over {w}_{0} $

Sinc Function

It is denoted as sinc(t) and it is defined as sinc

$$ (t) = {sin pi t over pi t} $$

$$ = 0, text{for t} = pm 1, pm 2, pm 3 … $$

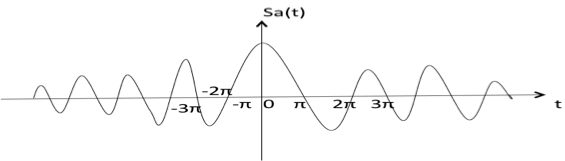
Sampling Function

It is denoted as sa(t) and it is defined as

$$sa(t) = {sin t over t}$$

$$= 0 ,, text{for t} = pm pi,, pm 2 pi,, pm 3 pi ,… $$