The range variation of σ for which the Laplace transform converges is called region of convergence.
Properties of ROC of Laplace Transform
-
ROC contains strip lines parallel to jω axis in s-plane.
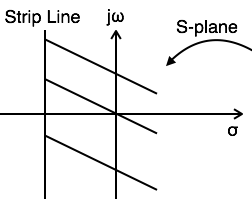
-
If x(t) is absolutely integral and it is of finite duration, then ROC is entire s-plane.
-
If x(t) is a right sided sequence then ROC : Re{s} > σo.
-
If x(t) is a left sided sequence then ROC : Re{s} < σo.
-
If x(t) is a two sided sequence then ROC is the combination of two regions.
ROC can be explained by making use of examples given below:
Example 1: Find the Laplace transform and ROC of $x(t) = e-^{at}u(t)$
$L.T[x(t)] = L.T[e-^{at}u(t)] = {1 over S+a}$
$ Re{} gt -a $
$ ROC:Re{s} gt >-a$
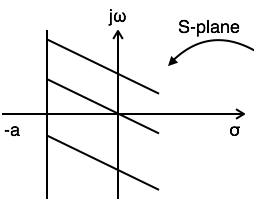
Example 2: Find the Laplace transform and ROC of $x(t) = e^{at}u(-t)$
$ L.T[x(t)] = L.T[e^{at}u(t)] = {1 over S-a} $
$ Re{s} < a $
$ ROC: Re{s} < a $
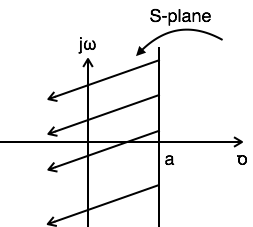
Example 3: Find the Laplace transform and ROC of $x(t) = e^{-at}u(t)+e^{at}u(-t)$
$L.T[x(t)] = L.T[e^{-at}u(t)+e^{at}u(-t)] = {1 over S+a} + {1 over S-a}$
For ${1 over S+a} Re{s} gt -a $
For ${1 over S-a} Re{s} lt a $
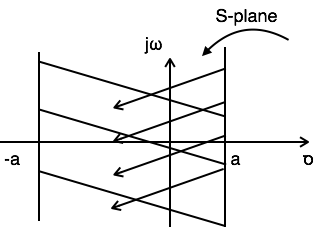
Referring to the above diagram, combination region lies from –a to a. Hence,
$ ROC: -a < Re{s} < a $
Causality and Stability
-
For a system to be causal, all poles of its transfer function must be right half of s-plane.
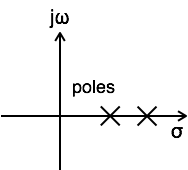
-
A system is said to be stable when all poles of its transfer function lay on the left half of s-plane.
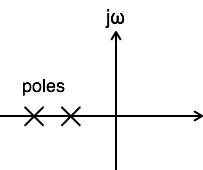
-
A system is said to be unstable when at least one pole of its transfer function is shifted to the right half of s-plane.
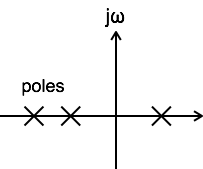
-
A system is said to be marginally stable when at least one pole of its transfer function lies on the jω axis of s-plane.
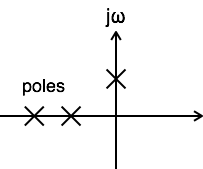
ROC of Basic Functions
| f(t) | F(s) | ROC |
|---|---|---|
| $u(t)$ | $${1over s}$$ | ROC: Re{s} > 0 |
| $ t, u(t) $ | $${1over s^2} $$ | ROC:Re{s} > 0 |
| $ t^n, u(t) $ | $$ {n! over s^{n+1}} $$ | ROC:Re{s} > 0 |
| $ e^{at}, u(t) $ | $$ {1over s-a} $$ | ROC:Re{s} > a |
| $ e^{-at}, u(t) $ | $$ {1over s+a} $$ | ROC:Re{s} > -a |
| $ e^{at}, u(t) $ | $$ – {1over s-a} $$ | ROC:Re{s} < a |
| $ e^{-at}, u(-t) $ | $$ – {1over s+a} $$ | ROC:Re{s} < -a |
| $ t, e^{at}, u(t) $ | $$ {1 over (s-a)^2} $$ | ROC:Re{s} > a |
| $ t^{n} e^{at}, u(t) $ | $$ {n! over (s-a)^{n+1}} $$ | ROC:Re{s} > a |
| $ t, e^{-at}, u(t) $ | $$ {1 over (s+a)^2} $$ | ROC:Re{s} > -a |
| $ t^n, e^{-at}, u(t) $ | $${n! over (s+a)^{n+1}} $$ | ROC:Re{s} > -a |
| $ t, e^{at}, u(-t) $ | $$ – {1 over (s-a)^2} $$ | ROC:Re{s} < a |
| $ t^n, e^{at}, u(-t) $ | $$ – {n! over (s-a)^{n+1}} $$ | ROC:Re{s} < a |
| $ t, e^{-at},u(-t) $ | $$ – {1 over (s+a)^2} $$ | ROC:Re{s} < -a |
| $ t^n, e^{-at}, u(-t) $ | $$ – {n! over (s+a)^{n+1}} $$ | ROC:Re{s} < -a |
| $ e^{-at} cos , bt $ | $$ {s+a over (s+a)^2 + b^2 } $$ | |
| $ e^{-at} sin, bt $ | $$ {b over (s+a)^2 + b^2 } $$ |
Learning working make money