The state space model of Linear Time-Invariant (LTI) system can be represented as,

$$dot{X}=AX+BU$$

$$Y=CX+DU$$

The first and the second equations are known as state equation and output equation respectively.

Where,

• X and $dot{X}$ are the state vector and the differential state vector respectively.

• U and Y are input vector and output vector respectively.

• A is the system matrix.

• B and C are the input and the output matrices.

• D is the feed-forward matrix.

Basic Concepts of State Space Model

The following basic terminology involved in this chapter.

State

It is a group of variables, which summarizes the history of the system in order to predict the future values (outputs).

State Variable

The number of the state variables required is equal to the number of the storage elements present in the system.

Examples − current flowing through inductor, voltage across capacitor

State Vector

It is a vector, which contains the state variables as elements.

In the earlier chapters, we have discussed two mathematical models of the control systems. Those are the differential equation model and the transfer function model. The state space model can be obtained from any one of these two mathematical models. Let us now discuss these two methods one by one.

State Space Model from Differential Equation

Consider the following series of the RLC circuit. It is having an input voltage, $v_i(t)$ and the current flowing through the circuit is $i(t)$.

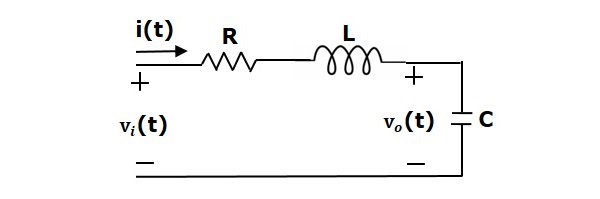
There are two storage elements (inductor and capacitor) in this circuit. So, the number of the state variables is equal to two and these state variables are the current flowing through the inductor, $i(t)$ and the voltage across capacitor, $v_c(t)$.

From the circuit, the output voltage, $v_0(t)$ is equal to the voltage across capacitor, $v_c(t)$.

$$v_0(t)=v_c(t)$$

Apply KVL around the loop.

$$v_i(t)=Ri(t)+Lfrac{text{d}i(t)}{text{d}t}+v_c(t)$$

$$Rightarrow frac{text{d}i(t)}{text{d}t}=-frac{Ri(t)}{L}-frac{v_c(t)}{L}+frac{v_i(t)}{L}$$

The voltage across the capacitor is –

$$v_c(t)=frac{1}{C} int i(t) dt$$

Differentiate the above equation with respect to time.

$$frac{text{d}v_c(t)}{text{d}t}=frac{i(t)}{C}$$

State vector, $X=begin{bmatrix}i(t) \v_c(t) end{bmatrix}$

Differential state vector, $dot{X}=begin{bmatrix}frac{text{d}i(t)}{text{d}t} \frac{text{d}v_c(t)}{text{d}t} end{bmatrix}$

We can arrange the differential equations and output equation into the standard form of state space model as,

$$dot{X}=begin{bmatrix}frac{text{d}i(t)}{text{d}t} \frac{text{d}v_c(t)}{text{d}t} end{bmatrix}=begin{bmatrix}-frac{R}{L} & -frac{1}{L} \frac{1}{C} & 0 end{bmatrix}begin{bmatrix}i(t) \v_c(t) end{bmatrix}+begin{bmatrix}frac{1}{L} \0 end{bmatrix}begin{bmatrix}v_i(t) end{bmatrix}$$

$$Y=begin{bmatrix}0 & 1 end{bmatrix}begin{bmatrix}i(t) \v_c(t) end{bmatrix}$$

Where,

$$A=begin{bmatrix}-frac{R}{L} & -frac{1}{L} \frac{1}{C} & 0 end{bmatrix}, : B=begin{bmatrix}frac{1}{L} \0 end{bmatrix}, : C=begin{bmatrix}0 & 1 end{bmatrix} : and : D=begin{bmatrix}0 end{bmatrix}$$

State Space Model from Transfer Function

Consider the two types of transfer functions based on the type of terms present in the numerator.

• Transfer function having constant term in Numerator.
• Transfer function having polynomial function of ‘s’ in Numerator.

Transfer function having constant term in Numerator

Consider the following transfer function of a system

$$frac{Y(s)}{U(s)}=frac{b_0}{s^n+a_{n-1}s^{n-1}+…+a_1s+a_0}$$

Rearrange, the above equation as

$$(s^n+a_{n-1}s^{n-1}+…+a_0)Y(s)=b_0 U(s)$$

Apply inverse Laplace transform on both sides.

$$frac{text{d}^ny(t)}{text{d}t^n}+a_{n-1}frac{text{d}^{n-1}y(t)}{text{d}t^{n-1}}+…+a_1frac{text{d}y(t)}{text{d}t}+a_0y(t)=b_0 u(t)$$

Let

$$y(t)=x_1$$

$$frac{text{d}y(t)}{text{d}t}=x_2=dot{x}_1$$

$$frac{text{d}^2y(t)}{text{d}t^2}=x_3=dot{x}_2$$

$$.$$

$$.$$

$$.$$

$$frac{text{d}^{n-1}y(t)}{text{d}t^{n-1}}=x_n=dot{x}_{n-1}$$

$$frac{text{d}^ny(t)}{text{d}t^n}=dot{x}_n$$

and $u(t)=u$

Then,

$$dot{x}_n+a_{n-1}x_n+…+a_1x_2+a_0x_1=b_0 u$$

From the above equation, we can write the following state equation.

$$dot{x}_n=-a_0x_1-a_1x_2-…-a_{n-1}x_n+b_0 u$$

The output equation is –

$$y(t)=y=x_1$$

The state space model is –

$dot{X}=begin{bmatrix}dot{x}_1 \dot{x}_2 \vdots \dot{x}_{n-1} \dot{x}_n end{bmatrix}$

$$=begin{bmatrix}0 & 1 & 0 & dotso & 0 & 0 \0 & 0 & 1 & dotso & 0 & 0 \vdots & vdots & vdots & dotso & vdots & vdots \ 0 & 0 & 0 & dotso & 0 & 1 \-a_0 & -a_1 & -a_2 & dotso & -a_{n-2} & -a_{n-1} end{bmatrix} begin{bmatrix}x_1 \x_2 \vdots \x_{n-1} \x_n end{bmatrix}+begin{bmatrix}0 \0 \vdots \0 \b_0 end{bmatrix}begin{bmatrix}u end{bmatrix}$$

$$Y=begin{bmatrix}1 & 0 & dotso & 0 & 0 end{bmatrix}begin{bmatrix}x_1 \x_2 \vdots \x_{n-1} \x_n end{bmatrix}$$

Here, $D=left [ 0 right ].$

Example

Find the state space model for the system having transfer function.

$$frac{Y(s)}{U(s)}=frac{1}{s^2+s+1}$$

Rearrange, the above equation as,

$$(s^2+s+1)Y(s)=U(s)$$

Apply inverse Laplace transform on both the sides.

$$frac{text{d}^2y(t)}{text{d}t^2}+frac{text{d}y(t)}{text{d}t}+y(t)=u(t)$$

Let

$$y(t)=x_1$$

$$frac{text{d}y(t)}{text{d}t}=x_2=dot{x}_1$$

and $u(t)=u$

Then, the state equation is

$$dot{x}_2=-x_1-x_2+u$$

The output equation is

$$y(t)=y=x_1$$

The state space model is

$$dot{X}=begin{bmatrix}dot{x}_1 \dot{x}_2 end{bmatrix}=begin{bmatrix}0 & 1 \-1 & -1 end{bmatrix}begin{bmatrix}x_1 \x_2 end{bmatrix}+begin{bmatrix}0 \1 end{bmatrix}left [u right ]$$

$$Y=begin{bmatrix}1 & 0 end{bmatrix}begin{bmatrix}x_1 \x_2 end{bmatrix}$$

Transfer function having polynomial function of ‘s’ in Numerator

Consider the following transfer function of a system

$$frac{Y(s)}{U(s)}=frac{b_n s^n+b_{n-1}s^{n-1}+…+b_1s+b_0}{s^n+a_{n-1}s^{n-1}+…+a_1 s+a_0}$$

$$Rightarrow frac{Y(s)}{U(s)}=left( frac{1}{s^n+a_{n-1}s^{n-1}+…+a_1 s+a_0} right )(b_n s^n+b_{n-1}s^{n-1}+…+b_1s+b_0)$$

The above equation is in the form of product of transfer functions of two blocks, which are cascaded.

$$frac{Y(s)}{U(s)}=left(frac{V(s)}{U(s)} right ) left(frac{Y(s)}{V(s)} right )$$

Here,

$$frac{V(s)}{U(s)}=frac{1}{s^n+a_{n-1}s^{n-1}+…+a_1 s+a_0}$$

Rearrange, the above equation as

$$(s^n+a_{n-1}s^{n-1}+…+a_0)V(s)=U(s)$$

Apply inverse Laplace transform on both the sides.

$$frac{text{d}^nv(t)}{text{d}t^n}+a_{n-1}frac{text{d}^{n-1}v(t)}{text{d}t^{n-1}}+…+a_1 frac{text{d}v(t)}{text{d}t}+a_0v(t)=u(t)$$

Let

$$v(t)=x_1$$

$$frac{text{d}v((t)}{text{d}t}=x_2=dot{x}_1$$

$$frac{text{d}^2v(t)}{text{d}t^2}=x_3=dot{x}_2$$

$$.$$

$$.$$

$$.$$

$$frac{text{d}^{n-1}v(t)}{text{d}t^{n-1}}=x_n=dot{x}_{n-1}$$

$$frac{text{d}^nv(t)}{text{d}t^n}=dot{x}_n$$

and $u(t)=u$

Then, the state equation is

$$dot{x}_n=-a_0x_1-a_1x_2-…-a_{n-1}x_n+u$$

Consider,

$$frac{Y(s)}{V(s)}=b_ns^n+b_{n-1}s^{n-1}+…+b_1s+b_0$$

Rearrange, the above equation as

$$Y(s)=(b_ns^n+b_{n-1}s^{n-1}+…+b_1s+b_0)V(s)$$

Apply inverse Laplace transform on both the sides.

$$y(t)=b_nfrac{text{d}^nv(t)}{text{d}t^n}+b_{n-1}frac{text{d}^{n-1}v(t)}{text{d}t^{n-1}}+…+b_1frac{text{d}v(t)}{text{d}t}+b_0v(t)$$

By substituting the state variables and $y(t)=y$ in the above equation, will get the output equation as,

$$y=b_ndot{x}_n+b_{n-1}x_n+…+b_1x_2+b_0x_1$$

Substitute, $dot{x}_n$ value in the above equation.

$$y=b_n(-a_0x_1-a_1x_2-…-a_{n-1}x_n+u)+b_{n-1}x_n+…+b_1x_2+b_0x_1$$

$$y=(b_0-b_na_0)x_1+(b_1-b_na_1)x_2+…+(b_{n-1}-b_na_{n-1})x_n+b_n u$$

The state space model is

$dot{X}=begin{bmatrix}dot{x}_1 \dot{x}_2 \vdots \dot{x}_{n-1} \dot{x}_n end{bmatrix}$

$$=begin{bmatrix}0 & 1 & 0 & dotso & 0 & 0 \0 & 0 & 1 & dotso & 0 & 0 \vdots & vdots & vdots & dotso & vdots & vdots \ 0 & 0 & 0 & dotso & 0 & 1 \-a_0 & -a_1 & -a_2 & dotso & -a_{n-2} & -a_{n-1} end{bmatrix} begin{bmatrix}x_1 \x_2 \vdots \x_{n-1} \x_n end{bmatrix}+begin{bmatrix}0 \0 \vdots \0 \b_0 end{bmatrix}begin{bmatrix}u end{bmatrix}$$

$$Y=[b_0-b_na_0 quad b_1-b_na_1 quad … quad b_{n-2}-b_na_{n-2} quad b_{n-1}-b_na_{n-1}]begin{bmatrix}x_1 \x_2 \vdots \x_{n-1} \x_n end{bmatrix}$$

If $b_n = 0$, then,

$$Y=[b_0 quad b_1 quad …quad b_{n-2} quad b_{n-1}]begin{bmatrix}x_1 \x_2 \vdots \x_{n-1} \x_n end{bmatrix}$$