SURF, which stands for Speeded−Up Robust Features, is an algorithm used to detect features. The SURF integral is a key concept within this algorithm.
To understand the SURF integral, let”s start with the idea of an image. An image is composed of pixels, which are tiny dots that store information about the intensity of the image at that particular location.
Now, imagine dividing the image into a small local neighborhood. The SURF integral is a way to efficiently calculate the total pixel value for each local neighborhood.
SURF Integral in Mahotas
In Mahotas, we can use the mahotas.features.surf.integral() function to compute the SURF integral of an image. Following is the basic approach of how the function works −
-
Initialization − First, the function initializes the integral image by setting all the pixel values to zero. Integral images refer to images that store the sum of all pixels up to a certain point.
-
Recursive Sum Calculation − The function then proceeds to calculate the sum of pixels for each point in the integral image. It does this recursively, meaning it calculates the sum for each point based on the previous sums.
As the integral images store the sum of all pixels up to a specific point, they can significantly increase the speed of computing SURF descriptors. Since the function uses recursion, it can be slow for computing the sum of large images.
The mahotas.features.surf.integral() function
The mahotas.features.surf.integral() function takes a grayscale image as input and returns an integral image as output.
The returned result is a new image, typically in the form of a NumPy array, where each pixel value corresponds to the sum of pixel intensities up to that pixel location.
Syntax
Following is the basic syntax of the surf.integral() function in mahotas −
mahotas.features.surf.integral(f, in_place=False, dtype=<class ''numpy.float64''>)
Where,
-
f − It is the input image.
-
in_place (optional) − It a flag which determines whether to overwrite the input image (default is ”False”).
-
dtype (optional) − It specifies the data type of the output image (default is float64).
Example
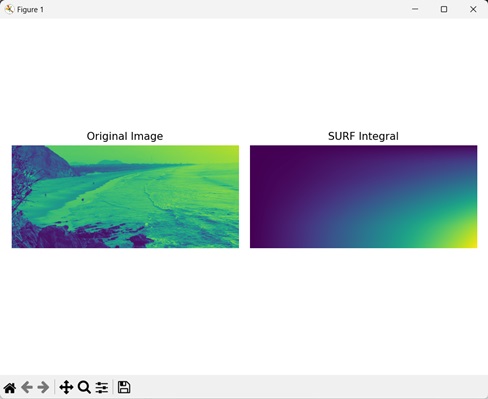
In the following example, we are calculating the SURF integral of an image using the mh.features.surf.integral() function.
import mahotas as mh
from mahotas.features import surf
import numpy as np
import matplotlib.pyplot as mtplt
# Loading the image
image = mh.imread(''sea.bmp'')
# Converting it to grayscale
image = mh.colors.rgb2gray(image)
# Getting the SURF integral
surf_integral = surf.integral(image)
# Creating a figure and axes for subplots
fig, axes = mtplt.subplots(1, 2)
# Displaying the original image
axes[0].imshow(image)
axes[0].set_title(''Original Image'')
axes[0].set_axis_off()
# Displaying the surf integral
axes[1].imshow(surf_integral)
axes[1].set_title(''SURF Integral'')
axes[1].set_axis_off()
# Adjusting spacing between subplots
mtplt.tight_layout()
# Showing the figures
mtplt.show()
Output
Following is the output of the above code −
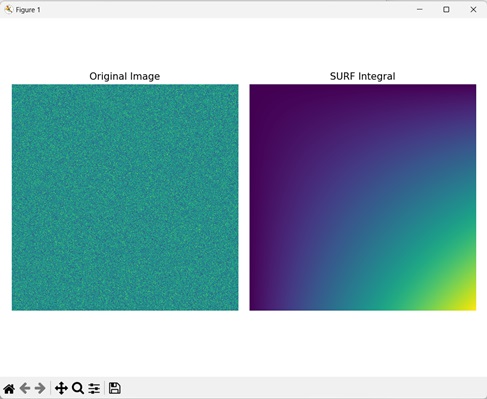
SURF Integral of a Random Image
We can also compute SURF integral of a randomly generate two−dimensional image. A two−dimensional random image refers to an image where each pixel is assigned a random intensity value. The intensity value can range from 0 (black) to 255 (white).
In mahotas, to create a 2−D random image we first specify its dimensions. Then, we pass these dimensions along with the intensity range of the pixels to np.random.randint() function.
After that we can compute the SURF integral of the image using the surf.integral() function.
Example
In the example mentioned below, we are computing the SURF integral of a randomly generated 2−D image.
import mahotas as mh
from mahotas.features import surf
import numpy as np
import matplotlib.pyplot as mtplt
# Specifying dimensions of image
l, w = 1000, 1000
# Creating a random 2-D image
image = np.random.randint(0, 256, (l, w))
# Getting the SURF integral
surf_integral = surf.integral(image)
# Creating a figure and axes for subplots
fig, axes = mtplt.subplots(1, 2)
# Displaying the original image
axes[0].imshow(image)
axes[0].set_title(''Original Image'')
axes[0].set_axis_off()
# Displaying the surf integral
axes[1].imshow(surf_integral)
axes[1].set_title(''SURF Integral'')
axes[1].set_axis_off()
# Adjusting spacing between subplots
mtplt.tight_layout()
# Showing the figures
mtplt.show()
Output
Output of the above code is as follows −
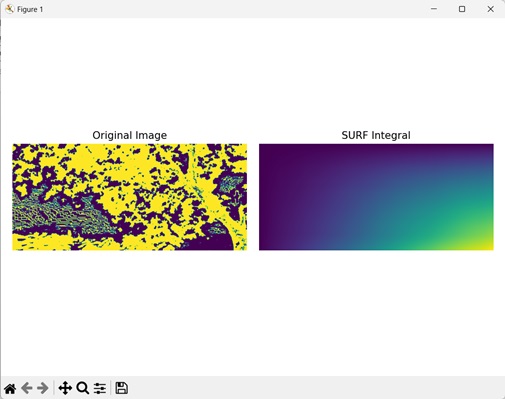
SURF Integral of a Threshold Image
In addition to random 2−D images, we can also compute the SURF integral of a threshold image. A threshold image is a binary image where the pixels are classified into the foreground or the background.
The foreground pixels are white and represented by the value 1, while the background pixels are black and represented by value 0.
In mahotas, we first threshold the input image using any thresholding algorithm. Let us assume . This can be done by using the mh.thresholding.bernsen() function on a grayscale image. Then, we can compute the SURF integral of threshold image using the surf.integral() function.
Example
In here, we are calculating SURF integral of a threshold image.
import mahotas as mh
from mahotas.features import surf
import numpy as np
import matplotlib.pyplot as mtplt
# Loading the image
image = mh.imread(''tree.tiff'')
# Converting it to grayscale
image = mh.colors.rgb2gray(image)
# Thresholding the image
image = mh.thresholding.bernsen(image, 5, 5)
# Getting the SURF integral
surf_integral = surf.integral(image)
# Creating a figure and axes for subplots
fig, axes = mtplt.subplots(1, 2)
# Displaying the original image
axes[0].imshow(image)
axes[0].set_title(''Original Image'')
axes[0].set_axis_off()
# Displaying the surf integral
axes[1].imshow(surf_integral)
axes[1].set_title(''SURF Integral'')
axes[1].set_axis_off()
# Adjusting spacing between subplots
mtplt.tight_layout()
# Showing the figures
mtplt.show()
Output
After executing the above code, we get the following output −