Statement: A continuous time signal can be represented in its samples and can be recovered back when sampling frequency f_s is greater than or equal to the twice the highest frequency component of message signal. i. e.

$$ f_s geq 2 f_m. $$

Proof: Consider a continuous time signal x(t). The spectrum of x(t) is a band limited to f_m Hz i.e. the spectrum of x(t) is zero for |ω|>ω_m.

Sampling of input signal x(t) can be obtained by multiplying x(t) with an impulse train δ(t) of period T_s. The output of multiplier is a discrete signal called sampled signal which is represented with y(t) in the following diagrams:

Here, you can observe that the sampled signal takes the period of impulse. The process of sampling can be explained by the following mathematical expression:

$ text{Sampled signal}, y(t) = x(t) . delta(t) ,,…,…(1) $

The trigonometric Fourier series representation of $delta$(t) is given by

$ delta(t)= a_0 + Sigma_{n=1}^{infty}(a_n cos⁡ nomega_s t + b_n sin⁡ nomega_s t ),,…,…(2) $

Where $ a_0 = {1over T_s} int_{-T over 2}^{ T over 2} delta (t)dt = {1over T_s} delta(0) = {1over T_s} $

$ a_n = {2 over T_s} int_{-T over 2}^{T over 2} delta (t) cos nomega_s, dt = { 2 over T_2} delta (0) cos n omega_s 0 = {2 over T}$

$b_n = {2 over T_s} int_{-T over 2}^{T over 2} delta(t) sin⁡ nomega_s t, dt = {2 over T_s} delta(0) sin⁡ nomega_s 0 = 0 $

Substitute above values in equation 2.

$therefore, delta(t)= {1 over T_s} + Sigma_{n=1}^{infty} ( { 2 over T_s} cos ⁡ nomega_s t+0)$

Substitute δ(t) in equation 1.

$to y(t) = x(t) . delta(t) $

$ = x(t) [{1 over T_s} + Sigma_{n=1}^{infty}({2 over T_s} cos nomega_s t) ] $

$ = {1 over T_s} [x(t) + 2 Sigma_{n=1}^{infty} (cos nomega_s t) x(t) ] $

$ y(t) = {1 over T_s} [x(t) + 2cos omega_s t.x(t) + 2 cos 2omega_st.x(t) + 2 cos 3omega_s t.x(t) ,…, …,] $

Take Fourier transform on both sides.

$Y(omega) = {1 over T_s} [X(omega)+X(omega-omega_s )+X(omega+omega_s )+X(omega-2omega_s )+X(omega+2omega_s )+ ,…] $

$therefore,, Y(omega) = {1over T_s} Sigma_{n=-infty}^{infty} X(omega – nomega_s )quadquad where ,,n= 0,pm1,pm2,… $

To reconstruct x(t), you must recover input signal spectrum X(ω) from sampled signal spectrum Y(ω), which is possible when there is no overlapping between the cycles of Y(ω).

Possibility of sampled frequency spectrum with different conditions is given by the following diagrams:

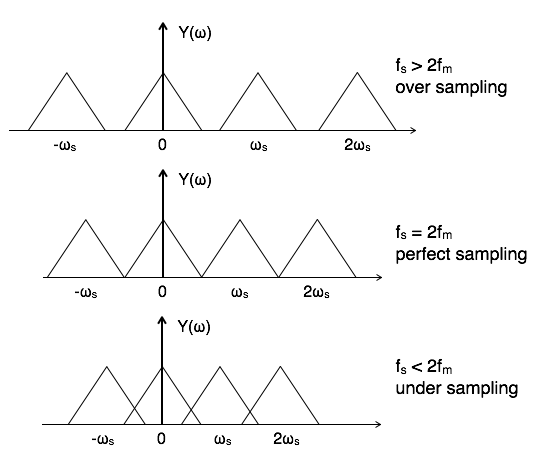
Aliasing Effect

The overlapped region in case of under sampling represents aliasing effect, which can be removed by

• considering f_s >2f_m

• By using anti aliasing filters.