In the previous chapter, we discussed that in an electromechanical energy conversion device, there is a medium of coupling between electrical and mechanical systems. In most of practical devices, magnetic field is used as the coupling medium. Therefore, an electromechanical energy conversion device comprises an electromagnetic system. Consequently, the energy stored in the coupling medium is in the form of the magnetic field. We can calculate the energy stored in the magnetic field of an electromechanical energy conversion system as described below.

Consider a coil having N turns of conductor wire wound around a magnetic core as shown in Figure-1. This coil is energized from a voltage source of v volts.

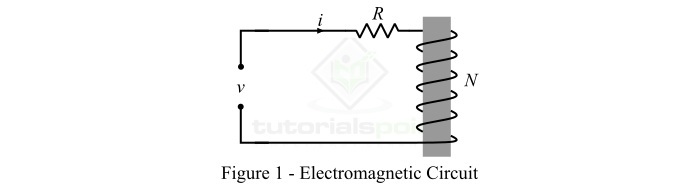
By applying KVL, the applied voltage to the coil to given by,

$$mathrm{mathit{V:=:e:+:iR}cdot cdot cdot (1)}$$

Where,

• e is induced EMF in the coil due to electromagnetic induction.

• R is the resistance of the coil circuit.

• $mathit{i}$ is the current flowing the coil.

The instantaneous power input to the electromagnetic system is given by,

$$mathrm{mathit{p}:=:mathit{Vi:=:ileft ( e+iR right )}}$$

$$mathrm{Rightarrow mathit{p}:=:mathit{ie+ i^{mathrm{2}}}mathit{R}cdot cdot cdot (2)}$$

Now, let a direct voltage is applied to the circuit at time t = 0 and that at end of t = t₁ seconds, and the current in the circuit has attained a value of I amperes. Then, during this time interval, the energy input the system is given by,

$$mathrm{mathit{W}_{in}:=:int_{0}^{t_{mathrm{1}}}:mathit{p:dt}}$$

$$mathrm{Rightarrow mathit{W}_{in}:=:int_{0}^{t_{mathrm{1}}}:mathit{ie:dt}:+:int_{0}^{t_{mathrm{1}}}mathit{i^{mathrm{2}}R:dt}cdot cdot cdot (3)}$$

From Equation-3, it is clear that the total input energy consists of two parts −

• The first part is the energy stored in the magnetic field.

• The second part is the energy dissipated due to electrical resistance of the coil.

Thus, the energy stored in the magnetic field of the system is,

$$mathrm{mathit{W}_{mathit{f}}:=:int_{0}^{t_{mathrm{1}}}:mathit{ie:dt}:cdot cdot cdot (4)}$$

According to Faraday’s law of electromagnetic induction, we have,

$$mathrm{mathit{e}:=:frac{mathit{dpsi }}{mathit{dt}}:=:frac{mathit{d}}{mathit{dt}}left ( mathit{Nphi } right ):=:mathit{N}frac{mathit{dphi }}{mathit{dt}}cdot cdot cdot (5)}$$

Where, $psi$ is the magnetic flux linkage and it is equal to $mathit{psi :=:Nphi }$.

$$mathrm{therefore mathit{W_{f}}:=:int_{0}^{mathit{t_{mathrm{1}}}}frac{mathit{dpsi }}{mathit{dt}}mathit{i:dt}}$$

$$mathrm{Rightarrow mathit{W_{f}}:=:int_{0}^{psi_{mathrm{1}}}mathit{i:dpsi }cdot cdot cdot (6)}$$

Therefore, the equation (6) shows that the energy stored in the magnetic field is equal to the area between the ($psi -i$) curve (i.e., magnetization curve) for the electromagnetic system and the flux linkage ($psi$) axis as shown in Figure-2.

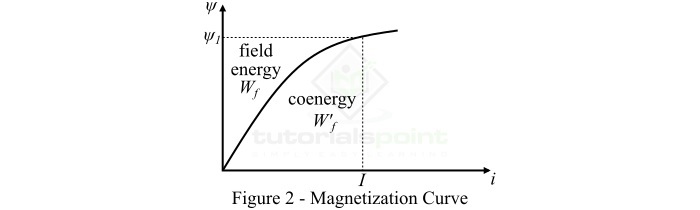
For a linear electromagnetic system, the energy stored in the magnetic field is given by,

$$mathrm{mathit{W_{f}}:=:int_{0}^{mathit{psi _{mathrm{1}}}}mathit{idpsi }:=:int_{0}^{psi_{mathrm{1}} }frac{psi }{mathit{L}}mathit{dpsi }}$$

Where, $psi:=:mathit{Nphi }:=:mathit{Li}$ and L is the self-inductance of the coil.

$$mathrm{therefore mathit{W_{f}}:=:frac{psi ^{mathrm{2}}}{2mathit{L}}:=:frac{1}{2}mathit{Li^{mathrm{2}}}cdot cdot cdot (7)}$$

Concept of Coenergy

Coenergy is an imaginary concept used to derive expressions for torque developed in an electromagnetic system. Thus, the coenergy has no physical significance in the system.

Basically, the coenergy is the area between the $psi -i$ curve and the current axis and is denoted by $mathit{W_{f}^{”}}$ as shown above in Figure-2.

Mathematically, the coenergy is given by,

$$mathrm{mathit{W_{f}^{”}}:=:int_{0}^{i}psi mathit{di}:=:int_{0}^{i}mathit{Li:di}}$$

$$mathrm{Rightarrow mathit{W_{f}^{”}}:=:frac{1}{2}mathit{Li^{mathrm{2}}}cdot cdot cdot (8)}$$

From equations (7) and (8), it is clear that for a linear magnetic system, the energy stored in the magnetic field and the coenergy are equal.