The operating performance of a three-phase induction motor can be explained with the help of the following two characteristics namely,
-
Torque-Slip Characteristics
-
Torque-Speed Characteristics
Torque Slip Characteristics of 3 Phase Induction Motor
The torque-slip characteristics of a three-phase induction motor is the curve drawn between the motor torque and slip for a particular value of rotor resistance. Figure-1 shows different torque-slip characteristics of a typical three-phase induction motor for a slip range from s = 0 to s= 1 for various values of rotor resistance.
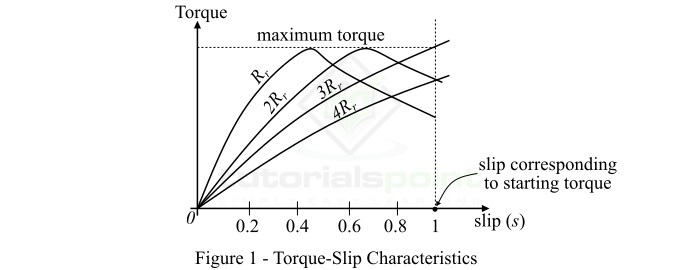
For a three-phase induction motor, the relation between the motor torque and slip under running condition is given by,
$$mathrm{mathit{tau _{r}}:=:frac{mathit{KsR_{r}}}{mathit{R_{r}^{mathrm{2}}+s^{mathrm{2}}X_{r}^{mathrm{2}}}}:cdot cdot cdot (1)}$$
Where,K is a constant,s is the slip, $mathit{R_{r}}$ is the per phase rotor resistance, and $mathit{X_{r}}$ is the standstill rotor reactance per phase.
From Equation-1, we may conclude the following points −
Case 1
If s = 0, then $mathit{tau _{r}}:=:0$. Therefore, the torque-slip curve starts from the origin.
Case 2
At normal speed of the motor, the slip is small, and thus $mathit{sX_{r}}$ is practically negligible as compared to $mathit{R_{r}}$.
$$mathrm{therefore mathit{tau _{r}}propto mathit{frac{s}{R_{r}}}}$$
Since for a given motor, $mathit{R_{r}}$ is also constant.
$$mathrm{therefore mathit{tau _{r}}propto mathit{s}}$$
Thus, the torque-slip curve is a straight line from zero slip to a slip that corresponds to full load.
Case 3
If slip value exceeds the full-load slip, then torque increases and becomes maximum when $mathit{R _{r}}:=:mathit{s:X_{r}}$. This maximum torque in a three-phase induction motor is known as breakdown torque or pull-out torque. The value of the breakdown torque is at least double of the full-load torque when the induction motor is operated at rated voltage and frequency.
Case 4
When the slip value becomes greater than that corresponding to the maximum torque, then the term $mathit{s^{mathrm{2}}:X_{r}^{mathrm{2}}}$ increases rapidly so that $mathit{R_{r}^{mathrm{2}}}$ may be neglected.
$$mathrm{therefore mathit{tau _{r}}propto mathit{frac{s}{s^{mathrm{2}}X_{r}^{mathrm{2}}}}}$$
As $mathit{X_{r}^{mathrm{2}}}$ is practically constant, then
$$mathrm{mathit{tau _{r}}propto mathit{frac{mathrm{1}}{s}}}$$
Hence, the torque is now inversely proportional to the slip. Thus, the torque-slip curve is a rectangular hyperbola.
Therefore, from the above analysis of torque-slip characteristics of a three-phase induction motor it is clear that the addition of resistance to the rotor circuit does not change the value of maximum torque, but it only changes the value of slip at which the maximum torque occurs.
Torque-Speed Characteristic of 3-Phase Induction Motor
For a three-phase induction motor, the motor torque depends upon the speed but we cannot express the relationship between them by a simple mathematical equation. Therefore, we use a torque-speed characteristic curve to show this relationship. Figure-2 shows a typical torque-speed characteristic curve of a three-phase induction motor.
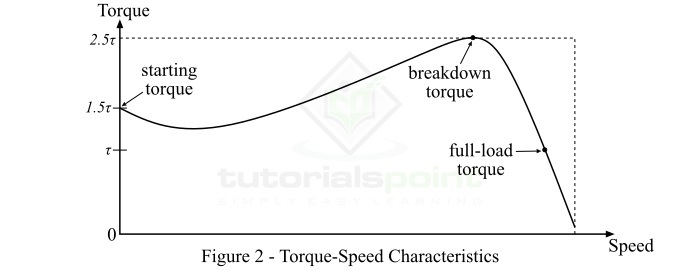
The following points may be noted from this characteristic curve −
-
If the full-load torque is $tau$, then the starting torque is $1.5tau $ and the maximum torque (or breakdown torque) is $2.5tau $
-
At full-load, if speed of the motor is N, and if the mechanical load on the shaft increases, the speed of the motor will drop until the motor torque is again equal to the load torque. Once the two torques are equal, the motor will run at a constant speed but lower than the previous. Although, if the motor torque becomes greater than $2.5tau $(i.e. breakdown torque), the motor will suddenly stop.
-
For a three-phase induction motor, the torque-speed curve is essentially a straight line between the points of no-load and full-load. The slope of the curve line depends upon the resistance of the rotor circuit, i.e., greater the resistance, the sharper the slope.
Learning working make money