This efficient use of memory is important for designing fast hardware to calculate the FFT. The term in-place computation is used to describe this memory usage.
Decimation in Time Sequence
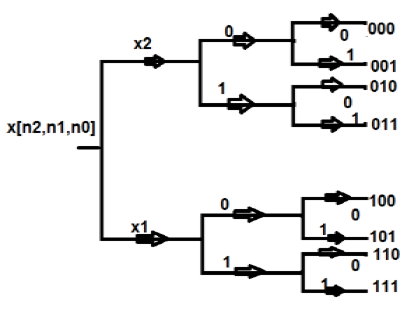
In this structure, we represent all the points in binary format i.e. in 0 and 1. Then, we reverse those structures. The sequence we get after that is known as bit reversal sequence. This is also known as decimation in time sequence. In-place computation of an eight-point DFT is shown in a tabular format as shown below −
| POINTS | BINARY FORMAT | REVERSAL | EQUIVALENT POINTS |
|---|---|---|---|
| 0 | 000 | 000 | 0 |
| 1 | 001 | 100 | 4 |
| 2 | 010 | 010 | 2 |
| 3 | 011 | 110 | 6 |
| 4 | 100 | 001 | 1 |
| 5 | 101 | 101 | 5 |
| 6 | 110 | 011 | 3 |
| 7 | 111 | 111 | 7 |
Decimation in Frequency Sequence
Apart from time sequence, an N-point sequence can also be represented in frequency. Let us take a four-point sequence to understand it better.
Let the sequence be $x[0], x[1], x[2], x[3], x[4], x[5], x[6], x[7]$. We will group two points into one group, initially. Mathematically, this sequence can be written as;
$$x[k] = sum_{n = 0}^{N-1}x[n]W_N^{n-k}$$
Now let us make one group of sequence number 0 to 3 and another group of sequence 4 to 7. Now, mathematically this can be shown as;
$$displaystylesumlimits_{n = 0}^{frac{N}{2}-1}x[n]W_N^{nk}+displaystylesumlimits_{n = N/2}^{N-1}x[n]W_N^{nk}$$
Let us replace n by r, where r = 0, 1 , 2….(N/2-1). Mathematically,
$$displaystylesumlimits_{n = 0}^{frac{N}{2}-1}x[r]W_{N/2}^{nr}$$
We take the first four points (x[0], x[1], x[2], x[3]) initially, and try to represent them mathematically as follows −
$sum_{n = 0}^3x[n]W_8^{nk}+sum_{n = 0}^3x[n+4]W_8^{(n+4)k}$
$= lbrace sum_{n = 0}^3x[n]+sum_{n = 0}^3x[n+4]W_8^{(4)k}rbrace times W_8^{nk}$
now $X[0] = sum_{n = 0}^3(X[n]+X[n+4])$
$X[1] = sum_{n = 0}^3(X[n]+X[n+4])W_8^{nk}$
$= [X[0]-X[4]+(X[1]-X[5])W_8^1+(X[2]-X[6])W_8^2+(X[3]-X[7])W_8^3$
We can further break it into two more parts, which means instead of breaking them as 4-point sequence, we can break them into 2-point sequence.
Learning working make money