In this chapter, we will understand what the Angular Diameter Distance is and how it helps in Cosmology.
For the present universe −
-
$Omega_{m,0} : = : 0.3$
-
$Omega_{wedge,0} : = : 0.69$
-
$Omega_{rad,0} : = : 0.01$
-
$Omega_{k,0} : = : 0$
We’ve studied two types of distances till now −
-
Proper distance (lp) − The distance that photons travel from the source to us, i.e., The Instantaneous distance.
-
Comoving distance (lc) − Distance between objects in a space which doesn’t expand, i.e., distance in a comoving frame of reference.
Distance as a Function of Redshift
Consider a galaxy which radiates a photon at time t1 which is detected by the observer at t0. We can write the proper distance to the galaxy as −
$$l_p = int_{t_1}^{t_0} cdt$$
Let the galaxy’s redshift be z,
$$Rightarrow frac{mathrm{d} z}{mathrm{d} t} = -frac{1}{a^2}frac{mathrm{d} a}{mathrm{d} t}$$
$$Rightarrow frac{mathrm{d} z}{mathrm{d} t} = -frac{frac{mathrm{d} a}{mathrm{d} t}}{a}frac{1}{a}$$
$$therefore frac{mathrm{d} z}{mathrm{d} t} = -frac{H(z)}{a}$$
Now, comoving distance of the galaxy at any time t will be −
$$l_c = frac{l_p}{a(t)}$$
$$l_c = int_{t_1}^{t_0} frac{cdt}{a(t)}$$
In terms of z,
$$l_c = int_{t_0}^{t_1} frac{cdz}{H(z)}$$
There are two ways to find distances, which are as follows −
Flux-Luminosity Relationship
$$F = frac{L}{4pi d^2}$$
where d is the distance at the source.
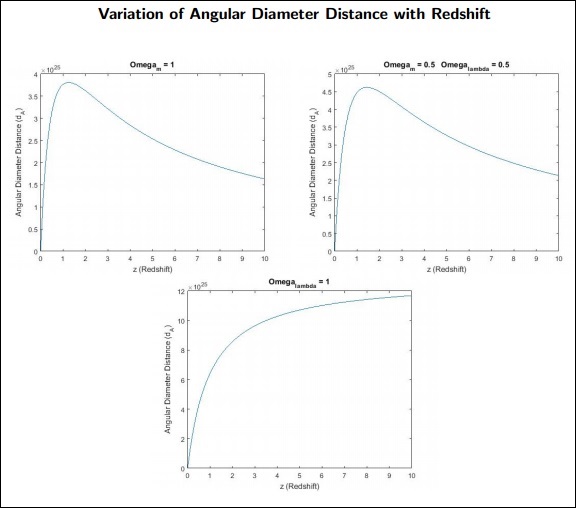
The Angular Diameter Distance of a Source
If we know a source’s size, its angular width will tell us its distance from the observer.
$$theta = frac{D}{l}$$
where l is the angular diameter distance of the source.
-
θ is the angular size of the source.
-
D is the size of the source.
Consider a galaxy of size D and angular size dθ.
We know that,
$$dtheta = frac{D}{d_A}$$
$$therefore D^2 = a(t)^2(r^2 dtheta^2) quad because dr^2 = 0; : dphi ^2 approx 0$$
$$Rightarrow D = a(t)rdtheta$$
Changing r to rc, the comoving distance of the galaxy, we have −
$$dtheta = frac{D}{r_ca(t)}$$
Here, if we choose t = t0, we end up measuring the present distance to the galaxy. But D is measured at the time of emission of the photon. Therefore, by using t = t0, we get a larger distance to the galaxy and hence an underestimation of its size. Therefore, we should use the time t1.
$$therefore dtheta = frac{D}{r_ca(t_1)}$$
Comparing this with the previous result, we get −
$$d_wedge = a(t_1)r_c$$
$$r_c = l_c = frac{d_wedge}{a(t_1)} = d_wedge(1+z_1) quad because 1+z_1 = frac{1}{a(t_1)}$$
Therefore,
$$d_wedge = frac{c}{1+z_1} int_{0}^{z_1} frac{dz}{H(z)}$$
dA is the Angular Diameter Distance for the object.
Points to Remember
-
If we know a source’s size, its angular width will tell us its distance from the observer.
-
Proper distance is the distance that photons travel from the source to us.
-
Comoving distance is the distance between objects in a space which doesn’t expand.
Learning working make money