The electronic circuits which perform the mathematical operations such as logarithm and anti-logarithm (exponential) with an amplification are called as Logarithmic amplifier and Anti-Logarithmic amplifier respectively.

This chapter discusses about the Logarithmic amplifier and Anti-Logarithmic amplifier in detail. Please note that these amplifiers fall under non-linear applications.

Logarithmic Amplifier

A logarithmic amplifier, or a log amplifier, is an electronic circuit that produces an output that is proportional to the logarithm of the applied input. This section discusses about the op-amp based logarithmic amplifier in detail.

An op-amp based logarithmic amplifier produces a voltage at the output, which is proportional to the logarithm of the voltage applied to the resistor connected to its inverting terminal. The circuit diagram of an op-amp based logarithmic amplifier is shown in the following figure −

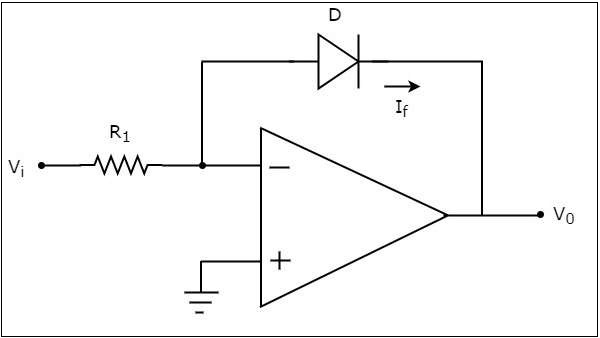
In the above circuit, the non-inverting input terminal of the op-amp is connected to ground. That means zero volts is applied at the non-inverting input terminal of the op-amp.

According to the virtual short concept, the voltage at the inverting input terminal of an op-amp will be equal to the voltage at its non-inverting input terminal. So, the voltage at the inverting input terminal will be zero volts.

The nodal equation at the inverting input terminal’s node is −

$$frac{0-V_i}{R_1}+I_{f}=0$$

$$=>I_{f}=frac{V_i}{R_1}……Equation 1$$

The following is the equation for current flowing through a diode, when it is in forward bias −

$$I_{f}=I_{s} e^{(frac{V_f}{nV_T})} ……Equation 2$$

where,

$I_{s}$ is the saturation current of the diode,

$V_{f}$ is the voltage drop across diode, when it is in forward bias,

$V_{T}$ is the diode’s thermal equivalent voltage.

The KVL equation around the feedback loop of the op amp will be −

$$0-V_{f}-V_{0}=0$$

$$=>V_{f}=-V_{0}$$

Substituting the value of $V_{f}$ in Equation 2, we get −

$$I_{f}=I_{s} e^{left(frac{-V_0}{nV_T}right)} ……Equation 3$$

Observe that the left hand side terms of both equation 1 and equation 3 are same. Hence, equate the right hand side term of those two equations as shown below −

$$frac{V_i}{R_1}=I_{s}e^{left(frac{-V_0}{nV_T}right)}$$

$$frac{V_i}{R_1I_s}= e^{left(frac{-V_0}{nV_T}right)}$$

Applying natural logarithm on both sides, we get −

$$Inleft(frac{V_i}{R_1I_s}right)= frac{-V_0}{nV_T}$$

$$V_{0}=-{nV_T}Inleft(frac{V_i}{R_1I_s}right)$$

Note that in the above equation, the parameters n, ${V_T}$ and $I_{s}$ are constants. So, the output voltage $V_{0}$ will be proportional to the natural logarithm of the input voltage $V_{i}$ for a fixed value of resistance $R_{1}$.

Therefore, the op-amp based logarithmic amplifier circuit discussed above will produce an output, which is proportional to the natural logarithm of the input voltage ${V_T}$, when ${R_1I_s}=1V$.

Observe that the output voltage $V_{0}$ has a negative sign, which indicates that there exists a 180⁰ phase difference between the input and the output.

Anti-Logarithmic Amplifier

An anti-logarithmic amplifier, or an anti-log amplifier, is an electronic circuit that produces an output that is proportional to the anti-logarithm of the applied input. This section discusses about the op-amp based anti-logarithmic amplifier in detail.

An op-amp based anti-logarithmic amplifier produces a voltage at the output, which is proportional to the anti-logarithm of the voltage that is applied to the diode connected to its inverting terminal.

The circuit diagram of an op-amp based anti-logarithmic amplifier is shown in the following figure −

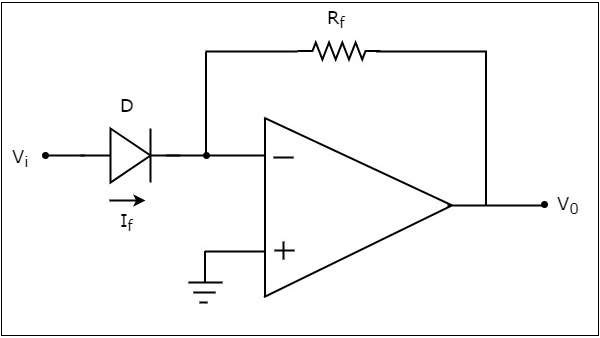
In the circuit shown above, the non-inverting input terminal of the op-amp is connected to ground. It means zero volts is applied to its non-inverting input terminal.

According to the virtual short concept, the voltage at the inverting input terminal of op-amp will be equal to the voltage present at its non-inverting input terminal. So, the voltage at its inverting input terminal will be zero volts.

The nodal equation at the inverting input terminal’s node is −

$$-I_{f}+frac{0-V_0}{R_f}=0$$

$$=>-frac{V_0}{R_f}=I_{f}$$

$$=>V_{0}=-R_{f}I_{f}………Equation 4$$

We know that the equation for the current flowing through a diode, when it is in forward bias, is as given below −

$$I_{f}=I_{s} e^{left(frac{V_f}{nV_T}right)}$$

Substituting the value of $I_{f}$ in Equation 4, we get

$$V_{0}=-R_{f}left {{I_{s} e^{left(frac{V_f}{nV_T}right)}}right }$$

$$V_{0}=-R_{f}{I_{s} e^{left(frac{V_f}{nV_T}right)}}……Equation 5$$

The KVL equation at the input side of the inverting terminal of the op amp will be

$$V_{i}-V_{f}=0$$

$$V_{f}=V_{i}$$

Substituting, the value of 𝑉𝑓 in the Equation 5, we get −

$$V_{0}=-R_{f}{I_{s} e^{left(frac{V_i}{nV_T}right)}}$$

Note that, in the above equation the parameters n, ${V_T}$ and $I_{s}$ are constants. So, the output voltage ${V_0}$ will be proportional to the anti-natural logarithm (exponential) of the input voltage ${V_i}$, for a fixed value of feedback resistance ${R_f}$.

Therefore, the op-amp based anti-logarithmic amplifier circuit discussed above will produce an output, which is proportional to the anti-natural logarithm (exponential) of the input voltage ${V_i}$ when, ${R_fI_s}= 1V$. Observe that the output voltage ${V_0}$ is having a negative sign, which indicates that there exists a 180⁰ phase difference between the input and the output.