We can use Thompson”s Construction to find out a Finite Automaton from a Regular Expression. We will reduce the regular expression into smallest regular expressions and converting these to NFA and finally to DFA.
Some basic RA expressions are the following −
Case 1 − For a regular expression ‘a’, we can construct the following FA −
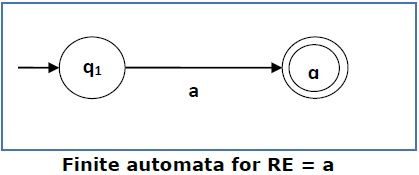
Case 2 − For a regular expression ‘ab’, we can construct the following FA −
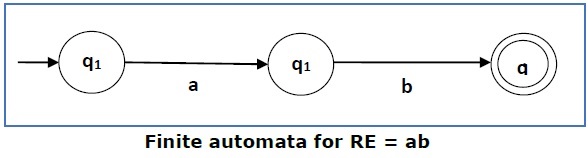
Case 3 − For a regular expression (a+b), we can construct the following FA −
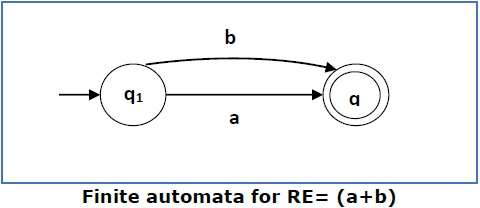
Case 4 − For a regular expression (a+b)*, we can construct the following FA −
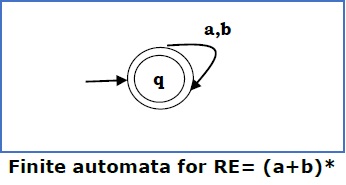
Method
Step 1 Construct an NFA with Null moves from the given regular expression.
Step 2 Remove Null transition from the NFA and convert it into its equivalent DFA.
Problem
Convert the following RA into its equivalent DFA − 1 (0 + 1)* 0
Solution
We will concatenate three expressions “1”, “(0 + 1)*” and “0”
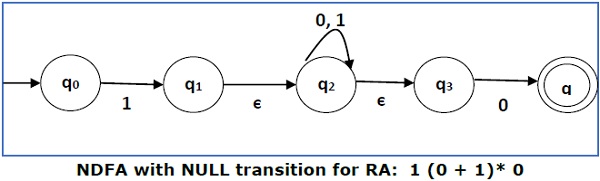
Now we will remove the ε transitions. After we remove the ε transitions from the NDFA, we get the following −
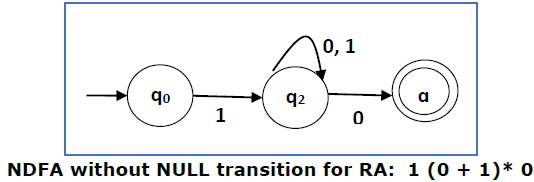
It is an NDFA corresponding to the RE − 1 (0 + 1)* 0. If you want to convert it into a DFA, simply apply the method of converting NDFA to DFA discussed in Chapter 1.
Finite Automata with Null Moves (NFA-ε)
A Finite Automaton with null moves (FA-ε) does transit not only after giving input from the alphabet set but also without any input symbol. This transition without input is called a null move.
An NFA-ε is represented formally by a 5-tuple (Q, ∑, δ, q0, F), consisting of
-
Q − a finite set of states
-
∑ − a finite set of input symbols
-
δ − a transition function δ : Q × (∑ ∪ {ε}) → 2Q
-
q0 − an initial state q0 ∈ Q
-
F − a set of final state/states of Q (F⊆Q).
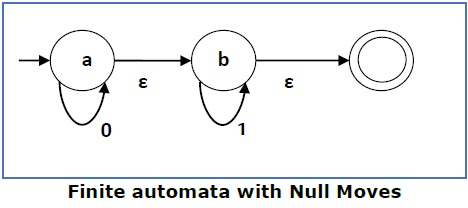
The above (FA-ε) accepts a string set − {0, 1, 01}
Removal of Null Moves from Finite Automata
If in an NDFA, there is ϵ-move between vertex X to vertex Y, we can remove it using the following steps −
- Find all the outgoing edges from Y.
- Copy all these edges starting from X without changing the edge labels.
- If X is an initial state, make Y also an initial state.
- If Y is a final state, make X also a final state.
Problem
Convert the following NFA-ε to NFA without Null move.
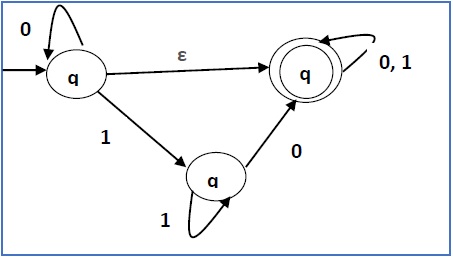
Solution
Step 1 −
Here the ε transition is between q1 and q2, so let q1 is X and qf is Y.
Here the outgoing edges from qf is to qf for inputs 0 and 1.
Step 2 −
Now we will Copy all these edges from q1 without changing the edges from qf and get the following FA −
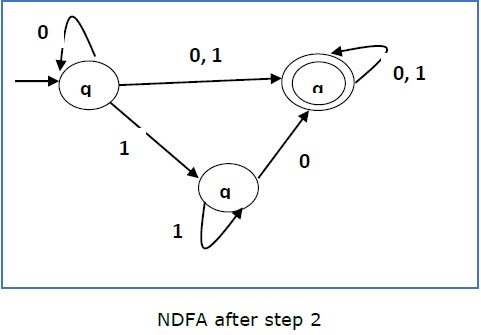
Step 3 −
Here q1 is an initial state, so we make qf also an initial state.
So the FA becomes −
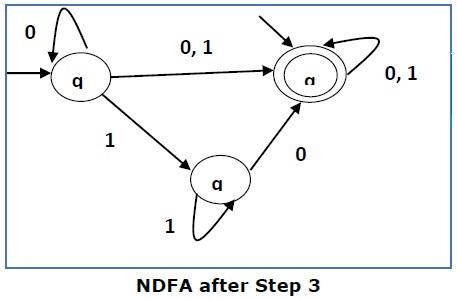
Step 4 −
Here qf is a final state, so we make q1 also a final state.
So the FA becomes −
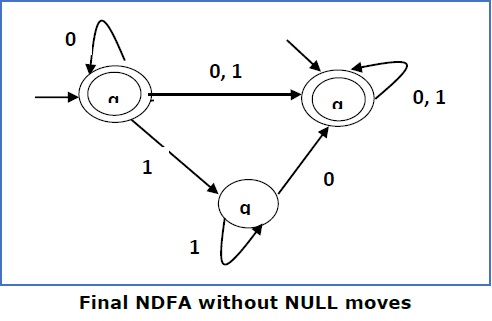
Learning working make money